ANTLR Tutorial – Part V

This is the fifth part of my ANTLR Tutorial. You can look at the previous issues here: Part I, Part II, Part III, and Part IV.

For this part, we will implement arithmetic expressions and mathematical functions (in fact, only a portion, as the remaining will be left as an exercise for the reader). To accomplish this we will need to:

1. Adapt the grammar for the new expressions;
2. Create new classes to store the arithmetic expression tree;
3. Create the visitors that create the expressions tree;
4. Create an evaluation process, that traverses the expression tree evaluating each operator and computing its result;
5. Create unit tests for evaluating and parsing expressions.

The reference of the LOGO arithmetic expressions is presented here. In this part of the tutorial, we will implement a subset of the syntax described in section 4.1. The next sections will be implemented as needed in future posts.

The Grammar

Everywhere we consider the use of a value, we can use an expression. Thus, the first step will be to edit every production we had that uses a value, replacing it with the expression token.

command : simpleCommand
        | SetPos squarePoint
        | SetXY simplePoint
        | Home
        | Arc expr expr
        ;

simpleCommand : cmd=(Right|Left|Forward|Back|SetX|SetY|SetH) expr ;

simplePoint : expr expr
            ;

squarePoint : '[' expr expr ']'
            ;

After this, we just need to define what an expression is. And an expression can be very different, as you can see in the documentation above. LOGO supports operators with a syntax similar to the previously defined for drawing commands, but also standard binary operators and even some LISP-style operators.

expr : cmd=(Sum|Difference|Product|Quotient|Power) expr expr  #prefixBinaryOp 
     | op=(Minus|'-') expr                                    #unaryMinus
     | '(' Sum expr+ ')'                                      #summation
     | '(' Product expr+ ')'                                  #product
     | '(' Quotient expr ')'                                  #quotient
     | <assoc=right> expr op='^' expr                         #binaryOp
     | <assoc=left> expr op=('*'|'/') expr                    #binaryOp
     | <assoc=left> expr op=('+'|'-') expr                    #binaryOp
     | value                                                  #scalar
     | '(' expr ')'                                           #scalar
     ;

Above we have the production for the set of arithmetic expressions I decided to support. The first thing you will notice is that every line has an identifier at the end of the line, that looks almost like a comment. They are not comments, but labels, that give each production alternative a name. This is useful when writing visitors. Instead of writing a single huge visitor for the whole production, each alternative with a different name will get its visitor.

Now, we’ll look into each type of operator:

• Line 1 supports operators in the LOGO syntax: Sum 2 4, Difference 4 5, and so on. They use a prefix or Polish notation, where the operator appears in the beginning, followed by the operands;
• Line 2 supports the LOGO syntax for the unary minus: Minus 4 but also the symbolic operator, - 4
• Lines 3 and 4 support a LISP-like syntax for summation and product. They allow a sequence for expressions to be added or multiplied. Equivalent to the mathematical \(\sum\) and \(\prod\).
• Line 5 is a strange quotient notation. (Quotient 4) is equivalent to \(\frac{1}{4}\). Thus, the only operand is the denominator.
• Lines 6 to 8 support binary operators in symbolic notation. There is a weird assoc annotation that will be described below.
• Finally, lines 9 and 10 state that a single value is also an expression and that an expression between parenthesis is still an expression.

Regarding the assoc annotation: parsers are not efficient when you have left-recursive productions. And they get even less efficient when you have rules that are both recursive at the left and the right.

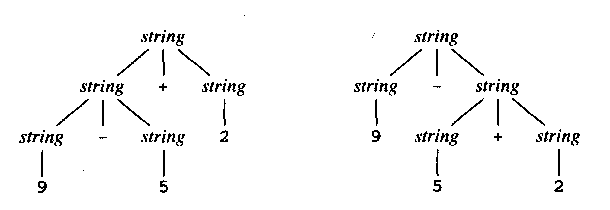
The image above shows two ways to recognize the expression \( 9 – 5 + 2 \) depending on the associativity you choose (left or right). If you do not specify which associativity to use, ANTLR will choose one by default. But it is a bad idea to let ANTLR choose. Mainly because it will not be clear to who is reading the grammar. Also, a different ANTLR version might choose another default value.

For the usual sum, subtraction, multiplication and division, associativity is usually at the left. But for the power, associativity is at the right. Mainly, because \( a ^ {b ^ c} = a ^ { (b^c) }\not= (a ^ b)^c\).

The next question you might ask is why we divided the three binary operators into three different alternatives. That’s because they have different precedence. When you have a multiplication and a sum in the same expression, the multiplication needs to be performed first, independently of it being at the left or right side of the sum. Thus, ANTLR uses the order you define the production alternatives to decide about priority.

Don’t forget to update the lexer to recognize the new commands:

Minus      : M I N U S ;
Power      : P O W E R ;
Quotient   : Q U O T I E N T ;
Product    : P R O D U C T ;
Difference : D I F F E R E N C E ;
Sum        : S U M ;

Storing the Expression Tree

To store the Abstract Syntax Tree of the expressions we will abuse the IParameter interface we created before. We will rename the IParameter.cs file to Parameter.cs, and change it from an interface to an abstract class. It will be helpful to hide the Execute method from all the parameter implementations so that they do not need to implement it themselves.

namespace Logo2Svg.AST;

public abstract class Parameter : INode
{
    public abstract float Value(Turtle turtle);
    public void Execute(Turtle turtle) => throw new NotImplementedException();
}

This class is small but will raise some interesting discussions. First, this is intended to be an abstract class, that every kind of parameter needs to implement. These parameters will not need to implement the Execute method but will need to implement a new one, named Value. This method will allow us to evaluate the parameter (that stores an expression). It returns a float value, which is the result of evaluating the expression. At the moment it receives the Turtle object, although, for this part of the tutorial, it will not be used at all.

The next step is to update ValueParam and the PointParam classes. The complete implementation of the first class follows.

using System.Globalization;

namespace Logo2Svg.AST;

public class ValueParam : Parameter
{
    private readonly float _value;
    public ValueParam(float value) =>_value = value;

    public override string ToString() => _value.ToString(CultureInfo.InvariantCulture);

    public override float Value(Turtle turtle) => _value;
}

We store the parameter value as a float value. The constructor just stores that value. We implement the stringification method, that converts the float to a string. Finally, the evaluation method. A float is evaluated to its value, and thus, we just return it.

Regarding the PointParam, we won’t have the evaluation as a float, but we will have a custom one to return an evaluated point:

using Logo2Svg.SVG;

namespace Logo2Svg.AST;

public class PointParam : Parameter
{
    private readonly Parameter _x, _y;

    public Point Point(Turtle t) => new Point(_x.Value(t), _y.Value(t));

    public PointParam(Parameter x, Parameter y)
    {
        _x = x;
        _y = y;
    }

    public override float Value(Turtle turtle) => throw new NotImplementedException();
    public override string ToString() => $"({_x},{_y})";
}

Here the Point method receives the turtle’s information so that the Value method can be called for both parameters. Note that the x and y components are stored as parameters and not as ParamValue instances. This is because a point might have a complex definition of each point, including arithmetic operations.

For all the arithmetic expressions (as well as the functions, although I will not describe them here), we will use a shared class, named ExprParam. Its implementation might resemble the Command class.

using Logo2Svg.Language;

namespace Logo2Svg.AST;

public class ExprParam : Parameter
{
    private readonly int _op;
    private readonly List<Parameter> _parameters;

    public ExprParam(int op, params Parameter[] parameters)
    {
        _op = op;
        _parameters = new List<Parameter>(parameters);
    }

    public override float Value(Turtle turtle)
    {
        var values = _parameters.Select(p => p.Value(turtle)).ToArray();
        return _op switch
        {
            LogoLexer.Sum => values.Aggregate(0f, (a, b) => a + b),
            LogoLexer.Difference => values[0] - values[1],
            LogoLexer.Minus => - values[0],
            // possible exception
            LogoLexer.Quotient => values.Length == 1 ?
                    1 / values[0] : values[0] / values[1],   
            LogoLexer.Product => values.Aggregate(1f, (a,b) => a * b),
            LogoLexer.Power => MathF.Pow(values[0], values[1]),
            _ => 0
        };
    }
    
    // stringification method here
  }

In terms of fields, we store an integer that represents the operation or function, as well as the list of parameters. Unlike the command class, we do not store the command in string form, just because there are too many variants. That’s also why I don’t share here the stringification method. To make it work properly we need some work, and the relevance to this tutorial is quite reduced.

The constructor just receives the data needed to fill in the fields. As for the evaluation method, we evaluate each parameter, storing its float values in an array. Then, we consider the different possible operators and perform the desired computation. Just note the quotient implementation, which works differently if only one parameter is present, as well as the unary minus implementation. Take care that we are not handling the possible division by zero.

These changes require us to update the Command.cs class as well. As the changes are simple, I will describe them here, instead of pasting the code:

• All references to IParameter are changed to Parameter
• Create a new function to retrieve a parameter value, evaluating it: private Parameter Parameter(int i) => Params[i];
• Taking into account the new function declared above, change all the lines from var value = Parameter(0).Value; to var value = Parameter(0).Value(turtle);
• Update the invocation to the Point accessor from turtle.Position = Parameter(0).Point; to turtle.Position = Parameter(0).Point(turtle);
• In the Arc implementation, replace Parameter(0).Value by Parameter(0).Value(turtle) (and similarly for parameter 1).

Visitors Implementation

In this section, I describe the visitors that need to be implemented, as well as the changes to the existing ones. We’ll start with the changes, and implement the new ones later.

All the visitors that use the value field, which was changed to expr, need to be updated, as follows:

  public override INode VisitSquarePoint([NotNull] LogoParser.SquarePointContext context)
  {
      var xVal = Visit<Parameter>(context.expr(0));
      var yVal = Visit<Parameter>(context.expr(1));
      return new PointParam(xVal, yVal);
  }

  public override INode VisitSimplePoint([NotNull] LogoParser.SimplePointContext context)
  {
      var xVal = Visit<Parameter>(context.expr(0));
      var yVal = Visit<Parameter>(context.expr(1));
      return new PointParam(xVal, yVal);
  }

  public override INode VisitSimpleCommand([NotNull] LogoParser.SimpleCommandContext context)
  {
      var param = Visit<Parameter>(context.expr());
      var command = context.cmd.Type;
      var name = context.cmd.Text;
      return new Command(command, name, param);
  }
  
  public override INode VisitCommand([NotNull] LogoParser.CommandContext context)
  {
      IToken command = null;
      List<Parameter> parameters = new();

      if (context.simpleCommand() is { } splCmd)
      {
          return Visit<Command>(splCmd);
      }

      if (context.Home() is { } homeCtx)
      {
          command = homeCtx.Symbol;
      }

      if (context.SetXY() is { } setXyCtx)
      {
          command = setXyCtx.Symbol;
          parameters.Add(Visit<Parameter>(context.simplePoint()));
      }

      if (context.SetPos() is { } setPosCtx)
      {
          command = setPosCtx.Symbol;
          parameters.Add(Visit<Parameter>(context.squarePoint()));
      }

      if (context.Arc() is { } argCtx)
      {
          command = argCtx.Symbol;
          parameters.AddRange(context.expr().Select(Visit<Parameter>));
      }

      return command is not null ? 
            new Command(command.Type, command.Text, parameters.ToArray()) : null;
  }

For the visitor for the scalar situation (the last two options of the production) we can implement this simple visitor. We just check which of the alternatives is present, and visit the appropriate one.

public override INode VisitScalar([NotNull] LogoParser.ScalarContext context)
{
    return context.value() is { } ctx ?
          Visit<Parameter>(ctx) : Visit<Parameter>(context.expr());
}

For the infix binary operator, the visitor is longer, but not too complicated. We visit the two parameters (taking advantage of Linq there) and then decide the correct token to use accordingly with the recognized character. The exception should never occur, but it is a good thing to have the exception there, in case we forget anything during the implementation.

public override INode VisitBinaryOp([NotNull] LogoParser.BinaryOpContext context)
{
    var parcels = context.expr().Select(Visit<Parameter>);
    int op = context.op.Text switch
    {
        "^" => LogoLexer.Power,
        "+" => LogoLexer.Sum,
        "-" => LogoLexer.Difference,
        "*" => LogoLexer.Product,
        "/" => LogoLexer.Quotient,
        _ => throw new ArgumentOutOfRangeException()
    };
    return new ExprParam(op, parcels.ToArray());
}

The unary minus has a similar implementation. Given that LOGO has a different keyword to distinguish from subtraction (difference) and the minus unary operator, we can use that to differentiate both commands.

public override INode VisitUnaryMinus([NotNull] LogoParser.UnaryMinusContext context)
{
    var sub = Visit<Parameter>(context.expr());
    return new ExprParam(LogoLexer.Minus, sub);
}

The LISP-style sum and product are simple as well. We just visit each parameter, and create a sum or a product of the entire list.

public override INode VisitSummation([NotNull] LogoParser.SummationContext context)
{
    var parcels = context.expr().Select(Visit<Parameter>);
    return new ExprParam(context.Sum().Symbol.Type, parcels.ToArray());
}

public override INode VisitProduct([NotNull] LogoParser.ProductContext context)
{
    var parcels = context.expr().Select(Visit<Parameter>);
    return new ExprParam(context.Product().Symbol.Type, parcels.ToArray());
}

The quotient is similar, but with only one parameter:

public override INode VisitQuotient([NotNull] LogoParser.QuotientContext context)
{
    return new ExprParam(context.Quotient().Symbol.Type, Visit<Parameter>(context.expr()));
}

And, finally, the visitor for the Polish notation:

public override INode VisitPrefixBinaryOp([NotNull] LogoParser.PrefixBinaryOpContext context)
{
    var parcels = context.expr().Select(Visit<Parameter>);
    return new ExprParam(context.cmd.Type, parcels.ToArray());
}

As you can see above, the visitors are all very similar. Implementing the remaining functions and operators is just following the same approach. You might even be able to reuse a large portion of the code.

Unit Testing

We should have started implementing unit testing earlier, but I had so many interesting things to discuss. But we will deal with that now. Unit testing, in C#, is usually implemented as a standalone project. Just like we did in the first part of this tutorial, we will use the command line to create the project. Just open a terminal, and get into the root folder of the solution.

dotnet new mstest -o LogoTests
dotnet sln Logo.sln add LogoTests/

The first line creates the new project, named LogoTests. It was created with the mstest framework. There are other alternatives that you can google about. I just opted for the more traditional one. The second line adds the project to the global solution.

Inside the folder, you should get two files (it might be different in previous or future versions of the package template), one named Usings.cs and one named UnitTest1.cs. The first file is used to include all the inclusion of modules that will be shared by the module. By default, it includes the inclusion of the Microsoft testing tools. The second file includes a sample unit test. Let’s start by renaming that file.

mv LogoTests/UnitTest1.cs LogoTests/Expressions.cs

In order to have the tests finding the implementation of the Logo2Svg project we need to create a link between the projects. That can be done using the dotnet command line tool as follows:

dotnet add LogoTests/ reference Logo2Svg/

This should be enough for the project to run smoothly. Let’s implement tests! Add the following content to the test file.

[TestClass]
public class Expressions
{
    [TestMethod]
    public void SimpleValue()
    {
        const float value = 10.4f;
        IParameter param = new ValueParam(value);
        
        Assert.AreEqual(value, param.Value(null), "Value correctly stored");
    }
}

We are declaring the class as a testing one, as well as a simple method, as a testing method. We declare a float value, that we will store in a parameter. We store that value and ask our code if, evaluating that parameter, we get the same original value. Note that we use null as the value for the turtle as, for now, it is not being used for anything. The third argument of the assertion method is used to write a debugging message of the running test.

You can run all tests with

dotnet test

I will not implement many tests. During the remaining parts of the tutorial, I might add more to the GIT repository. But the samples I will show here will be enough for you to understand the idea and be able to write your tests.

  [TestMethod]
  public void SumTwoValues()
  {
      const float a = 10.4f, b = 30.2f;
      ValueParam pA = new(a), pB = new(b);
      Parameter sum = new ExprParam(LogoLexer.Sum, pA, pB);
      
      Assert.AreEqual(a + b, sum.Value(null), "Sum correctly computed");
  }

  [TestMethod]
  public void SumMultipleValues()
  {
      var r = new Random(666);
      var values = Enumerable.Range(0, 10).Select(_ => r.NextSingle()).ToArray();
      var parameters = values.Select<float, Parameter>(v => new ValueParam(v)).ToArray();
      Parameter sumExpr = new ExprParam(LogoLexer.Sum, parameters);
      var sumValue = values.Aggregate(0f, (a, b) => a + b);

      Assert.AreEqual(sumValue, sumExpr.Value(null), "Sum correctly computed");
  }

These two methods test the sum operator. The first sums two values, and the second sums ten randomly generated ones.

More interesting than to test only the tree (this tests, basically, the evaluation portion of our code), is to test the complete process of parsing and evaluation. Let’s create a new file in the tests project, named ExpressionsParser.cs.

This time I will use parametrized tests, that allow us to test more than one feature with the same testing code. I will explain in a moment, in case you never used this technique. Add the following code to the new file:

using Antlr4.Runtime;
using Logo2Svg.AST;
using Logo2Svg.Language;

namespace LogoTests;

[TestClass]
public class ExpressionsParser
{
    [TestMethod]
    [DataRow("4", 4f)]
    [DataRow("4.5", 4.5f)]
    public void ParseValue(string expr, float value)
    {
        AntlrInputStream input = new AntlrInputStream(expr);
        var lexer = new LogoLexer(input);
        var parser = new LogoParser(new CommonTokenStream(lexer));

        var exprContext = parser.expr();
        var visitor = new TreeVisitor();
        var param = visitor.Visit<Parameter>(exprContext);

        var result = param.Value(null);
        Assert.AreEqual(value, result, $"Correctly parse of {expr}");
    }
}

Other than adding the boilerplate code, the test method now receives two parameters: a string, which will be the LOGO expression we want to evaluate, and a float, which is the result the expression should evaluate. Above the method, we have two DataRow lines. These lines specify two tests, one for the integer value 4, and the other for the float value 4.5. Do not forget to add the trailing f for literal float values in C#.

The testing code creates a LogoParser object and parses the testing string using the expr production. This is important (see line 19). We are just testing expressions, and therefore, we are just using the expression part of the LOGO grammar. Having the abstract syntax tree, we evaluate and compare it with the golden result.

Nevertheless, note that creating the parser at each step is tiresome. To simplify our testing writing, create the file TestUtils.cs with the following code:

using Antlr4.Runtime;
using Logo2Svg.AST;
using Logo2Svg.Language;

namespace LogoTests;

public static class TestUtils
{
    public static Parameter ToParameter(this string expr)
    {
        AntlrInputStream input = new AntlrInputStream(expr);
        var lexer = new LogoLexer(input);
        var parser = new LogoParser(new CommonTokenStream(lexer));

        var exprContext = parser.expr();
        var visitor = new TreeVisitor();
        return visitor.Visit<Parameter>(exprContext);
    }
}

This auxiliary extension method (see Microsoft documentation for a complete explanation of what an extension method is) evaluates a string and returns the AST for it, considering it is a valid LOGO parameter. With this method, we can create more tests easily. Add the following tests to the ExpressionsParser.cs file.

    [TestMethod]
    [DataRow("sum 4 3.2", 4+3.2f)]
    [DataRow("difference 4 3.2", 4-3.2f)]
    [DataRow("product 2 4.3", 2 * 4.3f)]
    [DataRow("quotient 3 2", 3f/2f)]
    [DataRow("power 2 3", 2*2*2f)]
    [DataRow("4 + 3.2", 4+3.2f)]
    [DataRow("3 - 2.1", 3-2.1f)]
    [DataRow("3 * 2.3", 3 * 2.3f)]
    [DataRow("2 / 4", 0.5f)]
    [DataRow("9.3 ^ 2", 9.3f*9.3f)]
    [DataRow("(sum 1 2 3 4 5 6 7 8 9)", 45f)]
    [DataRow("(product 4 3 2 1)", 24f)]
    [DataRow("(quotient 4)", 1/4f)]
    public void ParseBasicOperators(string expr, float value)
    {
        var param = expr.ToParameter();
        var result = param.Value(null);
        Assert.AreEqual(value, result, $"Correctly parse of {expr}");
    }

    
    [TestMethod]
    [DataRow("2 * 3 + 4", 10f)]
    [DataRow("4 + 3 * 2", 10f)]
    [DataRow("2 + 3 ^ 2", 11f)]
    [DataRow("3 ^ 2 + 2", 11f)]
    [DataRow("3 ^ 2 ^ 3", 6561f)]
    [DataRow("3 * - 2", -6f)]
    public void Priorities(string expr, float value)
    {
        var param = expr.ToParameter();
        var result = param.Value(null);
        Assert.AreEqual(value, result, $"Correctly priorities for {expr}");
    }

Can you see how easy is it to write tests using this auxiliary method? I also simplified our first test in the GIT. While we could join the two groups of tests in a single method I decided to have them separated, accordingly with their goals. The first is just to test simple operators, while the second mixes them to test their relative priorities.

Extra Implementation

During the next few days, I will add the following extra implementations in the GIT, which will not be discussed in this part of the tutorial or in future ones.

• The implementation for the remaining arithmetic operators and functions that are described on the LOGO page (except for the last two, which deal with lists);
• The stringification method for the ExprParam class (although a bit sloppy);
• Handling of the division by zero exception;
• Some more tests, including some to test only the AST generation of the expressions.